

When you use the loss function in these deep learning frameworks, you get automatic differentiation so you can easily learn weights that minimize the loss. The weighted Cross-Entropy loss function is used to solve the problem that the accuracy of the deep learning model overfitting on the test set due to the. A perfect model has a cross-entropy loss. The aim is to minimize the loss, i.e, the smaller the loss the better the model. The loss function comes out of the box in PyTorch and TensorFlow. Cross - entropy loss is used when adjusting model weights during training. This is the loss function used in (multinomial) logistic regression and extensions of it such as neural. Of course, you probably don’t need to implement binary cross entropy yourself. Log loss, aka logistic loss or cross-entropy loss. mean() method call in the implementation above.

#CROSS ENTROPY LOSS FUNCTION HOW TO#
For this reason, we typically apply the sigmoid activation function to raw model outputs. In this blog post, you will learn how to implement gradient descent on a linear classifier with a Softmax cross-entropy loss function With this combination. Since we’re taking np.log(yhat) and np.log(1 - yhat), we can’t use a model that predicts 0 or 1 for yhat.Notice the log function increasingly penalizes values as they approach the wrong end of the range. Here’s a plot with the first and second log terms (respectively) when they’re switched on: That would move the loss in the opposite direction that we want (since, for example, np.log(yhat) is larger when yhat is closer to 1 than 0) so we take the negative of the sum instead of the sum itself. weighted exponential or cross-entropy loss converge to the max-margin model. The y and (1 - y) terms act like switches so that np.log(yhat) is added when the true answer is “yes” and np.log(1 - yhat) is added when the true answer is “no”. Since improvements over cross-entropy could be observed in the experiments on all datasets, it can be concluded that any loss function that encourages. that can adapt to class imbalances by re-weighting the loss function during. That means you want to penalize values close to 0 when the label is 1 and you want to penalize values close to 1 when the label is 0. And the KullbackLeibler divergence is the difference between the Cross Entropy H for PQ and the true Entropy H. This is the Cross Entropy for distributions P, Q.
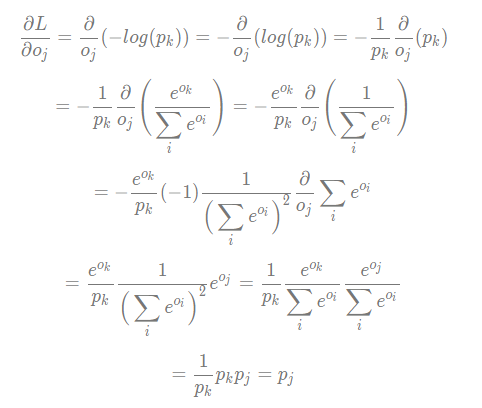
To train a good model, you want to penalize predictions that are far away from their ground truth values. The information content of outcomes (aka, the coding scheme used for that outcome) is based on Q, but the true distribution P is used as weights for calculating the expected Entropy. The data you use to train the algorithm will have labels that are either 0 or 1 ( y in the function above), since the answer for each record in your training data is known. When the model produces a floating point number between 0 and 1 ( yhat in the function above), you can often interpret that as p(y = 1) or the probability that the true answer for that record is “yes”. This is an elegant solution for training machine learning models, but the intuition is even simpler than that.īinary classifiers, such as logistic regression, predict yes/no target variables that are typically encoded as 1 (for yes) or 0 (for no). That is, we want to minimize the difference between ground truth labels and model predictions. We’re trying to minimize the difference between the y and yhat distributions. Good question! The motivation for this loss function comes from information theory. This is because the negative of the log-likelihood function is minimized. The cross-entropy loss function is also termed a log loss function when considering logistic regression. Return -(y * np.log(yhat) + (1 - y) * np.log(1 - yhat)).mean() Why does this work? The cross-entropy loss function is used as an optimization function to estimate parameters for logistic regression models or models which has softmax output. For multi-class classification tasks, cross entropy loss is a great candidate and perhaps the popular one See the screenshot below for a nice function of cross entropy loss. In this paper we describe and evolve a new loss function based on categorical cross-entropy. """Compute binary cross-entropy loss for a vector of predictionsĪn array with len(yhat) predictions between Īn array with len(y) labels where each is one of or corrected losses were presented in 7 and 17. Label_smoothing(y::Union) with eltype Bool:Ġ.43989f0 source binary_cross_entropy(yhat: np.ndarray, y: np.ndarray) -> float:


 0 kommentar(er)
0 kommentar(er)
